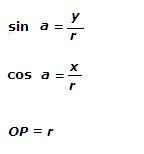Blah Blah

Okay, I know my previous posts are a little bit boring. So now, let's post something "interesting".

Right, so, did you ever come to this problem?

You just received your cool handphone, with its own built-in MP3 player, but to your disappointment, it's so freaking soft (even if the volume is at its max!)

The volume is already so high, you still want it to be more louder. But you want to do that without having to cough up a lot of money. So, did you have that kind of problem? If so, how are you gonna do that?

I've found a cheap way to amplify the volume of your phone by simply playing around with rubbish. It works for me, but not sure about you. Maybe it's just because of psychological reasons that I find it to me more louder using my method. But anyway, I think is not only me who knows about this stupid, lame and yet effective way to boost the volume of the handphone. Maybe some one else in this world might know about it.

Enough of the crap! Let's get down and dirty!!

You will need:

• A top-less aluminium can
• A handphone, which plays music

The cheapest aluminium can costs only about maybe RM1 to RM2. Just get a gas drink, finish it, wash it, cut the top off and you'll get a top-less can.

WARNING: Since the thin walls of the aluminium can may cut you if you're not careful, stick a cellophane tape around the rim of the can.

Okay, here is the photo of the items:


Steps:

1. Prepare your items
2. Examine your phone and look for the speaker hole. For my phone (Nokia 6300), the speaker is at the bottom. Then, start playing your MP3.
   
   
3. Gently place the phone into the can, and make sure that the speaker is facing towards the bottom of the can, not upwards. This way,the sound waves generated by the phone goes down towards the bottom of the can, reflect off the bottom of the can and back up and out of the can and into your ears. The sound waves might reflect back and forth a few times in the can before it can get out of the can. This can create the "reverberation" effect.
   
   
   
   
   

Due to the geometry of the can, most of the sound waves can be directed at one point, so that point can hear most of the sound. At other places, the sound is softer, but could still be heard clearly. Obviously, this is a very bad way of implementing the "Audio Spotlight" invented by... err, who's that again? Oh, see here:



But anyway, it works like a charm. It kinda amplifies the sound from the phone.

Desktop died!!

Finally, the desktop computer has died. Could the timing be any better? I wanna print the installation booklet already, then it died. What more? The installation booklet is in the desktop, and I only can use the printer through the desktop. Stupid!!

See, the desktop has been dying to die already. It has been crashing every now and then and survived for 2 months. Now, instead of crashing, it crashed and burned. So, I installed Windows 2000 on it so that I can use that desktop, but after installation, the desktop was lacking of driver. So, I can't use the printer and worst, I can't even use the speaker!!

Tried reinstalling Windows XP. But it crashed halfway through. I don't wanna reformat it and I will only do it as a last resort. I'll probably never reformat it anyway. My sister has like 1000+ MP3s and videos in there. You see how much can get lost by reformatting?

I suspect is a hardware failure. The hardware in the desktop is not very good already, but I'm not sure which hardware it is. Might be the RAM. So now, I'm trying my best to find solutions through the net.

UPDATE:
Hey, I finally got it to run!! I don't even know why did I do so many complicated things when I could have just re-installed Windows XP.

What I did was, I booted up the computer using the Windows XP CD, installed Windows XP on to my second Hard-Disk. It actually worked!!

Now, the speakers are still having problem, so I'll try to rectify it. Man, I feel like a computer technician already :D!!

OMG!! 2 weeks till Trials!!

Yup, there's around 2 more weeks till the dreaded trial, then another trial, and finally, the moment all the Form 3's had been fearing for the whole year, PMR, or in it's expanded form, Penilaian Menengah Rendah, or translated, Lower Secondary Assessments, or something like that. I am supposed to start studying by now, but it's just so freaking hard to concentrate. Let's review what I'm supposed to study:

• BM - The novels are quite important, there are, count 'em, 3 novels to study. Then there's the literature.
• BI - Phantom of the Opera & Dr. Jekyll. But I'll probably focus on Jekyll rather than the Phantom. Anyway, I don't really worry too much about BI, but I'm trying my best not to get too over-confident about it, which is not good.
  
• Maths - Ahh... the formulas. Exactly, how many must we remember again?
• Science - Hopefully my brain cells can cope with all the things I've learnt since Form 1. I think there's about over 20 chapters to study, no?
• Geo - omg!! Really hate this!! Apart from being incredibly hard to understand and memorise, it's incredibly annoying. Espeially Form 2. There are so many freaking things to remember. Oh yeah, musn't forget about Form 3. Form 3 Text Book lists out the "commonly" asked places and locations for things like mining areas, industrial areas, fisheries, and other blah things. Note the inverted quotation marks. Reference books are much better at listing out those places, since they list out more than the text book. And also, a lot of places aren't in the text book and those places are, quite frequently, the subject of many questions in the exam. Wait, wait, Form 1 also have the "different climates around the world" and the countries that are having those kind of climates. Easy? Not after you consider how much "ciri-ciri" you need to remember for every country listed out in the text book.
• History - History, let's see, exactly 11+8+7=26 chapters to study. That's about 1/2 the amount in the Geography syllabus. Still, that's quite a lot to study.
• Last, but not least, KH - In english, that's Living Skills or Life Skills or whatever skills. It's basically general knowledge on how things work and function and how to maintain everyay things. Sounds easy? Well, it's kinda easy when you talk about practical work, but when it comes to written tests, oh, there's a lot to remember.
  

So, let me count the amount of chapters I need to read: ±99 chapters altogether
Now, mind you, that doesn't include BI, BM, Maths and Science. I can't remember how many chapters there are in Science and Maths Form 1 and 2. So I didn't count them in.

Wow, 99 chapters for Geo, History and KH combined. 99 chapters in 2 weeks. That's like 99/14 days=about 7 chapters per day. My god!!!

Yeah, so that's about it.

Ooh!!

Okay, now the blog looks a little boring isn't it? I'm gonna add more images later to jazz things up a little. Now, if you can't see my blog properly, make sure your horizontal screen resolution is above 1000 pixels.

Hmm... I'm thinking Mr Ball's theme.

I've been wondering, since I have my own server now, what should I use it for? Should I make a chatting application like MSN Messenger, or maybe make an MMORPG (Massively-multiplayer online RPG) like Maple Story? My server seems a little useless. So, any suggestions?

Oh, and I have recorded the last level of BeeCatzArena (the modded game from the original game, Catz, which is not owned by me)

OMG!! Bee Lee's embarrassing moment!!

Right, the embarrassing moment is somewhere down here:
First - Second Period Period
Oh man!! It's PJ time. Blah!! Fortunately, today we played foot ball and volley ball only, no sit ups!!

Third Period
"Cikgu, boleh saya pergi jumpa Pn. Teh?"
then, the teacher nodded and signed my permission letter

Went out of the class, peeping at the Ko-op door.
"Dang, is it me, or does it look closed to me?"

So, I climbed to the 1st floor, took a look at the Ko-op again just to confirm that the Ko-op door is really closed. Walk towards the Teachers' Time table outside the teacher's room back door. Halfway walking, met Huey Wern, who was going to sent the attendance. So, walked with her towards the time table, then walked back towards the stairs, where we split up. It's seems that the teacher I was looking for isn't free at that time.

Right, so far so good. Nothing humiliating.

Fourth period
Nothing interesting really happened.

Recess!!
Got my KH Latihan book and the Interact Installation booklet. Walked with Jun Ray up to the Ko-op to see Pn Teh. Gave her the booklet to see. Then suddenly, a teacher walked pass by

"Morning Pn Cheryl!!"
"What did you call me?" then, gave me that "look"
"Pn Cheryl??...oh...OMG!!! Pn Shirley!! Sorry, Pn Shirley!!!"
Then she walked away.

Yeah, I called Pn Shirley, Pn Cheryl. You know how embarrassing that was?? I couldn't even stop thinking about it and feel awful. I know, Pn Shirley is nice and all, but it was incredibly insulting to call someone a different name isn't it?

Yeah, so that was what happened today. Now, yesterday, on the other hand:

Okay, it was BM. I just finished my BM Test, and wanna pass up my test paper. So, I gave the paper to my BM teacher, and so he said:
"Mana kertas jawapan? Saya hanya nak semak kertas jawapan?"

Now, my brain can't realy spontaneously react and choose me the right Malay words to say very quickly and so, my brain made me respond like this:
"Tak ada" with the hand-motion. (You know, the "nothing" or "don't have" gesture?"

And so, my mind told me after that:
"Yeah, Bee Lee, very nice choice of words!"

To me, saying "tak ada" is kinda impolite. But, in the end, I managed to pass up my paper (the kertas jawapan, that is).

Well, nobody's perfect I guess. Hey, that reminds me of a song by Miley Cyrus/Hannah Montana!! Yeah, I'm a big fan of her.

Blah...

Right... in my last post, I posted Trigonometry, right?? Okay, now, here is an implementation of what I said about in my previous post:

Updated Mr Ball!!

Now, if you're thinking, why am I still updating it after 3 months from it's last update already? It's kinda old news already isn't it? Well, old news to you lah. But to me, Mr Ball's the product of my 1.5 months of planning and programming. I'm not just gonna leave it there and catch dust inside my computer. It's one of my biggest achievements in Game Maker. That's the first ever 3D game I have made, so I wouldn't just let it go rot away in my Hard Disk. Haha.

Anyway, I was bored just now, and played a bit of Mr Ball to entertain myself. But I found 1 very bad flaw in Level 6, the Spear Diamond thingie. If you keep shooting it, even if it has reached its Counter-Attack Threshold, it won't counter you until it stops receiving hits from your water gun. That is not good, since it'll make the level end incredibly fast. Because of that, I just tweaked it, so, regardless of how long you can manage to keep shooting him, as long as the Counter Attack Threshold bar is filled up, it'll counter you. If the boss's HP is like 1000+ HP, I wouldn't even care about this problem, but this boss only has like 500HP, the lowest amount of HP for a boss in this game.

I got so bored, I decided to record my battle with that boss, and here it is!!



Now, let's talk Maths!! I just got nothing better to do anyway. OK, this math-mojo is actually related to the video above. How? Okay, if you've watched the video, and if you played other games, a lot of them has objects going around another object in a circle (Circular motion around an object in err... shorter terms).

If you hate maths, i suggest that you look away now. This is just to let time pass by me. So, here goes:

Now, this is just a method on how to make things move in a circle in a game.



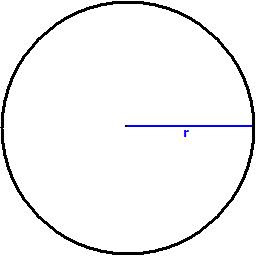
As you can see, that's a circle, right? Cool isn't it? I drew that in Microsoft Paint!! Haha. Yeah, I know, anyone can do better than that!! So, other than a circle, you should also be able to see the radius, marked "r". I hope you know trigonometry, because, I'm gonna go into trigs soon.

Right, the centre of the circle represents the position of Object A in a Cartesian Plane and the circle represents the series of points that Object B will move on. How do we make Object B move along those points on the circle? Haha, this is where Trigonometry comes in to play.

First, draw a line from the centre (O) to a point on a circle (P). When that line (OP) meets the circle, draw another line from the intersection point down to the radius, such that it intersects the radius perpendicularly, which will represent the y-coordinate of Point P relative to O. This is easier shown in graphics. Bring out Microsoft Paint again!!




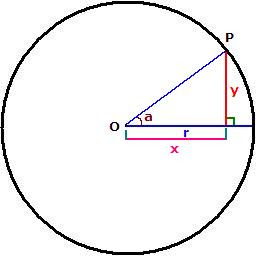
There you go!! You can also see how the x-thingie is formed. So, OP is the same as r because OP is also the radius. Now, the angle subtended at the centre is abbreviated a. Using trigonometry, we know that:



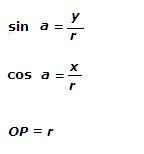
Okay, now, a is the direction of Point P from the centre. Yup, the direction. How do we find the x and y values of the Point P given the direction from centre O. Remember, a direction of 0° is pointing to the right. What do I mean by that? Erm... shit, how do I explain this?? Anyway, just keep in mind, 0° is right. Then, as the angle goes higher, the rotating point goes counter-clockwise around the centre O. So, 90° will be at the top, 180° will be to the left and 270° will be pointing towards the bottom.

Yeah, so, we have the centre O with points (x_o, y_o). We are also given an angle a, which is the direction of P from O and the radius. The radius is just the distance of point P from O. To find Point P's coordinates relative to O, we use the above trigonometric formulas.

The coordinates of Point P, relative to O, given the direction and distance of that point from O can be calculated using:
x_p=r cos a
y_p=r sin a

Now, keep in mind that those are coordinates of P relative to O. To convert x_p and y_p into "world" coordinates, ie, coordinates that are relative to the origin of the Cartesian plane (0,0), you must add both coordinates with the coordinates of point O.

So, the x-value of Point P on the Cartesian Plane is: x=x_o+r cos a
and the y value of Point P on the Cartesian Plane is: y=y_o+r sin a

So, that's some math to ponder your brain!!

Robotics Competition's tomorrow!!

Yup!! Going for Robotics Competition tomorrow!! Dang, I feel kinda pressured. I'm the only one in the 2 groups taking part in the competition who knows how to program the robot nicely. I don't get it, is it very hard to understand? It's just drag and drop only. Or maybe because I got experience in the "typing" style of programming. It didn't take me long to understand the so-called "RoboLAB" thingie. Not trying to be braggy lah. It's actually kinda hard to understand for beginners actually, I mean, the Help function doesn't really tell much in detail. It SUCKS! But if you play around with it, you'll soon get the hang of it. It's actually quite fun.

Okay, enough of that, now, what's the bright side of going such competitions? You get to skip lessons!! Muahaha!! I'm supposed to have a Science Diagnostics test tomorrow. Good luck to everyone who's sitting for that test!! While you guys are doing your test, I'll be busy having fun in an hour trip to Kuala Selangor!! Yup, the competition is in Kuala Selangor! On the way, you can see very beautiful scenery, with palm trees everywhere. Basically, you'll see a huge palm trees plantation area. The last time I went there, they aren't very big yet, maybe around a metre tall only. It's damn beautiful, especially with the blinding morning sun at the horizon!! Sorry for rubbing it in, for those who are sitting for the test!!

Sigh..

Right, last night, I went to Shannen's house to eat Barbecue!! Yup!! It was nice!! Except for the Spaghetti. It's not bad, it's just that I hate cheese. Overall, everything was good. Then after eating, we sat down at one corner, played "I have never" or whatever you call it. The rule is simple:

The player says about what he/she have never done before. If the other players have done that before, then they get punished!

And, what's the punishment? You must drink the sweet what-do-you-call-that-drink drink. I can't remember what's the drink called, but it's incredibly sweet. In the end, most of us found it boring, so we moved on to Truth or Dare. Everyone hated that sweet drink, well sorta, except for Kin Meng I think. Well, he sort of drank the left over in the bowl of the sweet substance. Anyway, moving on...

This morning, I went "hiking" with Mun Nee, Chia Sing and Shan Min to look for Sponsors for Interact Club Installation Day. We walked from Taman Megah all the way to SS2, then rode Chia Sing's mum's car back to Taman Megah, and back to school. Strangely, I only lost about 0.6kg from that. I thought I would have lost around 3!! LOL!! But, mind you, I'm not a weight-conscious freak. However, I do check my weight very frequently, because I wanna play with the new bathroom scale I have in my house.

So, after that, Shan Min and I went to Shannen's house to have fun. Well, for me at least. Shan Min got to copy some Civics project thingie down, then rush back to school. So, I hung out at Shannen's house until 4.15pm. Actually, I was supposed to go back at 3.00pm, but I got addicted to the Nintendo Wii. First, me and Amanda (yup, she was there, along with Li Ching and Kin Meng, but I think Kin Meng is more of a resident over there already, well, according to some people) played Ghost Squad. It's a first-person shooter, whereby you must aim with the WiiMote and shoot. I sucked at it and always get beaten by Amanda. *Cries* But at least it brought out the violent side of me!! (Sorta) I was like laughing insanely at one point while aimlessly shooting everywhere around the screen!! It's fun!!

Then, Li Ching, Amanda and I played the WiiSports games. It's amusing actually, but other than that, it's tiring, especially the boxing game. You got to keep doing the punching motion with your arms to win. Yeah, that was tiring. The characters in that game makes me laugh all the time. They are cute. And also, sometimes when they do something that I didn't expect them to do, I would laugh like mad.

And so, all the fun ended at 4.15. I went back home, watched a little TV, then started playing with my Robot. (Not really mine) I'm suppose to perfect the program to finish the track that was provided, but the problem is, the speed of the robot is so fast, it's not easy to get things right. Sigh... I got really stressed from that. I tried and tried again. When the robot just goes off to the wrong path, reset the robot and start again. It's so freaking fast until I can't really see what's really happening. Unfortunately, changing the speed of the robot to make it slower isn't the best choice, since I've got to make a lot of changes to time the robot. Yes, that's right, there's timing involved. But, without speed also not good, since the competition only gives me about 2 minutes to finish the course. That's kinda fast.

And what more? The robot got to grab an object at some point. And after grabbing, a lot of problems will turn up. The object feels light, but there's a lot of friction between that object and the playing field (the track), causing the robot to slow down and making all the turns useless.

I've got to finish up that program before Tuesday. And there's 1 more robot, which is currently not with me now. I can't test my program on that robot!! That's bad. I have to make a program specifically for one of the robots because the speeds are so different.

Sigh...

Stress... teenagers' worst nightmare

Now, let's go back in time, to the wonderful and happy day of Tuesday. So, Shannen and I planned to go out to eat Satay. In the afternoon, or rather, evening, I over-napped. So, I wanna call Shannen that I won't be going already. The problem is that

my handphone died!!

Why do I need my cellphone? It's because Shannen's number is in the phone. So, I went to look for my charger. But, I

lent my charger to my cousin brother

Okay, the problems are building up. Soon, the word slipped out of my mouth and I kinda like

told my father that I lent my charger to my cousin brother

Now, why is that bad? My father has this issue with my cousin living in my house, and doesn't really like it.

So, I borrowed my father's phone, exchanged sim cards. Turned on the phone, and you know what, I realized that

Shannen's number wasn't in my Sim Card!!

Called Jun Ray to ask for Shannen's number, but no luck. So, I gave up, but my father, sorta lectured me about "son, you shouldn't lend your phone to somebody else, if you know that your phone is gonna die. Besides, why should you even lend your own property to somebody else??". The nagging went on and on. I tried to keep my tears in, but my emotions surpassed my effort of trying to keep them in my heart. So, I shed some tears. I was really mad. I guess he didn't really understand me. I was trying to be generous, and my phone was incredibly full of energy when I lent my charger to my cousin. It's just that I played a game on my phone, so it died. But, I guess my father and I have different opinions, and he is just, somewhat, caring for me. So, I don't blame him. I love him, he's a part of the family. Still, I don't really agree with what he said. But, might as well let it go. It's futile trying to argue with the head of the family.

Now, here's the start of the stress. After that incident, I got really guilty. I spewed out the message that my cousin borrowed my charger to my father. And because of that, I was incredibly scared that my father would scold him. I really don't want that to happen. Seeing family members fight in front of me can really tear my heart into pieces. As much as I hate it, I just don't have the right to stop it. I shouldn't be a busy body and barge into other people's issues. But, if I don't stop the fight, I fear my family might drift apart. That's a bit too serious isn't it, more of like jumping to conclusions. But, I just can't stop thinking the worst. I'm an incredibly sensitive person, in terms of emotions.

Fortunately, my cousin didn't get a scolding, I think. I slept early that day so I won't see anything serious happening. But I guess, nothing really happened. Okay, that's Tuesday. Now, Wednesday...

During Interact Club meeting, I accidentally ruined Audrey's group's Civics project. I did apologize, but, it wasn't enough. Even if Audrey forgave me that time and said "Oh, nevermind lah", I just can't get over my guilt. I destroyed somebody else's project and not doing anything about it, apart from saying sorry. When I came back home, I called Miu Yinn to tell her about the problem and asked if it's restore-able. But, she deleted the photos in her computer already. So I was like, "Oh shit... what have I done...". The whole day I couldn't stop forgetting about that project I ruined. The whole day I was thinking "What can I do?? I am so careless!!"

Today, I wanted to apologize to Audrey about the whole project thing again. But after David advised me that I should get over my guilt, I reconsidered. David told me, sooner or later, she'll forget about it. So I thought, if I apologized again, I'll remind her about the ruined project. Dang, if her gang gets low marks for the project. I'll be seriously upset, because I was the one responsible of destroying the project. Sigh... I'm a very careless person. No?

Right, that's not the end. Oh no. I got these things to finish

1. Civics project. I gave Shannen the things to type, and she's gonna type the project. But I'm still quite worried.
2. Robotics. I'm going for the National Robotics Competition next week, Tuesday. The Lego robot still doesn't work really well. I just don't know what to do...
3. Finish up the program booklet for Interact Installation Day. Yeah, my job is just to retype everything and print it out, then get 50 photocopies of it, but, still, the dateline is next week. I'm waiting for my friend to finish everything up and send them to me.

Sigh... I've never hand so much stress in one week. I'm not in a good mood now. Man, if only life is better than this. I guess, life can never always be nice to you.

Tales of Phantasia Progress

Okay, I've finally reached around 1/3 of th game. Just defeated Dhaos, the evil evil guy who you must defeat in order to win. But, this is just only the first big battle of the game. I'm not gonna tell too much as this might spoil some people who are playing the game. The battle was quite long, about 7 minutes.

As you can see through the video below, I got a little trouble after Cless died. In the end, I managed to win that rather annoying bossfight. I was lucky not to get pummeled by the so-called "Dhaos Laser" (interesting, isn't it?). Okay fine, I did get hurt once by the Dhaos Laser. As long as I keep "kacau-ing" him, he won't be able to execute many spells, and that dreaded "Dhaos Laser".

Hmm... where did the BLProductions Wonderland go?

Okay, I find having 3 blogs is a bit mafan. So I just scrapped it away. Now, I can spend more time hanging out in my own blog and 3D blog. Oh, yeah. I just remembered something...

Remember the game I was talking about? Mr Ball? Now, I recorded a video on the game that started all that.



That is BeeCatzArena. Now, I've got to be honest. Originally, that is not my game. The owner of the original game is Gogs Productions. I just modded it for fun. My cousin and I had a lot of fun modifying the game, but we didn't release the game because we've stolen a lot of stuff, namely, the graphics. Like the sprite of the cat (the player), it's not drawn by me. So, that's why, it'll never be released into the wild. It's just for entertainment purposes for me only.

Now, how can that inspire me to start making a 3D game? A lot of things were incorporated into Mr Ball, for example, the spears, the ice stalagmite, the diamond, the water gun and lots more. I had a lot of fun making Mr Ball Arena.

Okay now, let's talk about how the secret battle ever came to be. A lot of RPGs I played have those optional boss battles that you can win to get cool things for your characters. That is what made me place an optional boss battle in the game that you can only access if you have the password, which you can get after defeating the final boss. The fun thing about creating an insanely hard secret boss is that you don't need to take the "balance of power" into consideration. I mean, in a normal battle, I must make the battles possible to win, but not so simple. So, the boss' power must not be so good, and the attacks must not be so lethal.

But, the insane version of the secret battle is not meant to be won. Why? Come on, all games must have at least a way to win, right? Err... I guess, but the insane secret boss is merely just for fun. It's just to test how good you are in the game, and how long you could survive. So, since it is not meant to be won, I can go nuts with the boss's attacks and also it's AI. If you've watched the video I posted, somewhere halfway through the video (I think) shows the recently added desperation attack. No, not the one with the evil laugh, it's the one when the diamond go floats up in the air, then recites an incantation and then all the spears come flying out from nowhere. Now, that really highlights my true mean-ness in creating harsh attacks. But, that isn't really my limit yet. I can go further in designing deadlier attacks.

Okay, 1 more thing. About the voices. In this video, you can't hear many voices. The only 3 man-made voices in this game are the evil laughter, sort of a"taunting" speech and err... some kind of an incantation. Would you believe that I made the evil laughter? .... Haha, joking only. But, the latter two voices are actually my voice. "But Bee Lee, they don't sound like your voice!!" Yeah, I know. That's where technology comes into play. I altered my voice because I'm no good voice actor, and my voice's a bit odd in the microphone, so, I changed my voice and added a little reverberation!! Lol. What did I say actually? Yeah, it's a bit fuzzy, but this is what I said:

"Know what true power is!"

"Oh lord of darkness, give me your power and bring my enemies to their destined annihilation!"

Yeah, that's it. Hope you liked it. I'll post more videos of this game soon. So, I hope you liked it.

Civics project rocks!

Yup, that's right! This year's Civics assignment rocks! We have to go eat, and take picture of the food we eat to complete our project. Oh wait, we also need to type out the report and blah, but still, the eating part's the best! Wanna know what happened today while my gang and I went to eat? You can check out the post below this one!! Got pictures as well!!

Today's Civics Project "Report"

Summary of what happened today!

Okay, my group, consisting of me, Shannen, David and Shamand, came to eat at some mamak stalls for our civics project. Unfortunately, Shamand wasn't able to come, so, only us 3 amigos were there to fill up our "food list".

David's order came first. He ordered Roti Canai. Quite nice. In the end, we ordered 2 Roti Canais because Shannen loved the Roti Canai.

Next comes Shannen's order, Roti Tisu. It's not really a tissue, right? Yeah, it's not a tissue, how fortunate.

Oh, and there's my Murtabak. Not very nice. There were BONES in it!!! What the hell?? I hurt my gum because I had never expected to have bones in my Murtabak ayam.

These were our drinks. 2 Teh Tarik (pull tea?? Okay, it sounds much better in Malay! Lol!) and 1 watermelon juice (mine!!). The juice was quite sweet, too sweet for me, but still okay lah. Can you find the hidden mickey?

We walked to a Chinese restaurant after that. We ate "Chap fan" or economy/mixed rice to some of you. Quite delicious. We shared 1 plate of Chap Fan. Felt quite awkward while eating.

I hate "Chap Fan" -Shannen

Enlarged photograph of the hard-boiled egg. Looks disgusting up-close, doesn't it? But it's incredibly delicious.

The empty plate. No idea why I had taken a photo of it.

Let's eat one more plate! -Shannen

Shows human's best way to die. Smoking!! I really hate smokers. I have this "issue" with smokers. Even if it's my father. If I just see anyone who smokes, I can get really annoyed, since I am getting more of the effects than the smoker himself.

Interest is what makes us continue on with our passion

Now, I rarely talk about what I love to do. A lot of people think that I love to study, study and study. In fact, a lot of my friends assume that I study a lot, and maybe even a bookworm. Actually, I'm not. I don't really study much. Everyday, after school, I will be on the computer, if not, PS2. It's very rare for you (and even me) to see me picking up a book and read. Obviously, this is not the way to go, but it's just very hard for me to study. I only study when the exams are near.

What else? Singing?? Yeah, I know. Very ironic. How can a guy like me sing? Actually, I can't really sing that well, but, come on, singing is not just about showing off right? It's about having fun. I never sing in public or whenever there's people around me. It might be because of my shyness, that's why I'm scared to sing to people around me. But, if I'm left alone, I turn my volume up high and sing, but obviously, I won't sing until the whole neighbourhood breaks down and probably bring the sky down. Lol!

My biggest interest, and probably my passion, is programming. I've been doing it since Standard 6, which is about 3 years ago. So, I'm probably an intermediate programmer now. I've never expected myself to be a programmer. This is the chain of events that sparked this interest:

1. Got introduced to Game Maker through a show called "Screen Savers" in TechTV (now G4TechTV or something, well, I think it's G4). TechTV was a channel in ASTRO. It's no longer in ASTRO today. Sigh...
2. I used Game Maker, and created a lot of crappy games (hey, I've got to start somewhere right?)
3. Later, I asked my dad to go look for the Delphi programming language. Why?? Because Game Maker was written in Delphi so I thought I'll be easy for me to write my own Game Maker as well. (in the end, I found out it wasn't that easy). In the computer shop, I got introduced to Visual Basic by the shopkeeper. It's an easy programming language. Little did that guy know, he gave me a disc containing the whole Visual Studio 2006 (not just Visual Basic), that means, it contains other "Visual" programming languages as well. Haha.
4. I played around with Visual Basic. After a few months, I thought of going higher, so I installed Visual C++. I got frustrated at the language, because it wasn't easy to learn. In the end, I gave up.
5. When I'm Form 1, I got the Delphi programming language, but it wasn't easy for me to pick it up since I'm already to used to the Visual Basic programming environment. I totally ditched Delphi.
6. I'm not sure when this happened, but I suddenly got introduced to Visual Basic .NET. I think it's when I searched around MSDN. I found out that Microsoft is giving free downloads for the public who wants to learn programming. The "Express" versions of the programming languages may have some limitations, but they still can make very sophisticated programs. And there I was, downloading Visual Basic Express 2005.
7. Few months later, I downloaded Visual C# Express 2005, and started learning that language from scratch. It wasn't hard. I wonder why.
8. Until now, C# is my programming language of choice.

Apart from those programming languages, I also learned Game Maker Language for, well... Game Maker, since you can't make complicated games without it. Nowadays, I'm concentrating a lot in Game Maker because I wanna finish up my games.

I also have a little experience with HTML, Javascript and CSS, because I was very fond of having a website of my own last time. Now, I can finally put them to good use.

Okay, so, what have I said? Right, so I like playing computer/PS2 and programming (be it software programming or web development). Don't worry, my list of interests doesn't stop there. I'll probably won't place watching TV as an interest here though. Don't ask me why, even though I love to watch TV.

I love animations. But, 1 thing for sure, my arts aren't beautiful, and my graphics are very "cacat". Even so, I've never grew tired of drawing for my games. Now, I've indulge myself into Flash animations. It's incredibly cool. I also have a 3D modelling program called Blender 3D (free from the net). It can also animate 3D scenes. I seldom play with it these days, but it's very fun. What made me interested in 3D animation is Animusic. It's a company producing 3D animations, synchronized with music (hence the name, Animusic). It's incredibly cool. I've thought of trying to make one but it's quite tough. So I'll leave it for later in the future, if I'm even willing to try. Here's an example: it's called "Pipe Dream" from the first Animusic DVD


Cool isn't it? I love that piece a lot. Same goes for the "Pipe Dream" from the 2nd DVD from Animusic. Whoa, ball bearings making music. If anyone were to do that, I'll do anything to see it (well, maybe I'll do things that are morally correct for me)

Those are some of my interests. I can't think of anymore now. I just got one question, am I the only software programmer in SMKTS? It's a bit lonely for me to be the only programmer in the school that I go to everyday. Sigh...

OMG!! What I've always wanted!

Ahh... I finally have Macromedia Flash MX 2004. Yes, it's a bit outdated, but it's still useful. I can finally make Flash movies!! Gosh... my drawing skills isn't very good. Especially on the comp. Hmm... maybe, the first thing I'll do is make the BLProductions Logo!! Muahahaha!!!